pyradiobiology is a package for radiobiological modeling (TCP, NTCP, EUD, gEUD) with Python.
It provides:
- Linear quadratic model for survival fraction and biological effective dose calculation
- Tumor Control Probability (TCP) models: linear-quadratic Poisson, empirical Poisson
- Normal Tissue Complication Probability (NTCP) model: Relative seriality (RS), Lyman-Kutcher-Burman (LKB)
- Generalized Equi-effective Uniform Dose (gEUD), Equi-effective Uniform Dose (EUD)
To install the package, just run:
pip install pyradiobiology
TcpEmpirical model
The TCP emipirical model or linear-quadratic Poisson model is given by:
\( P(D) = P(EQD_{2Gy}) = exp(-e^{eγ – (EQD_{2Gy}/D_{50})*(eγ-lnln2)}) \)
\(P(D)\) is the tumour control probability, when the tumour is homogenously irradiated at the total dose D and \(EQD_{2Gy}\) is the equi-effective dose at 2Gy per fraction of the total dose D when delivered at a fraction dose d.
\(\bf{D_{50}}\) is the dose in Gy, defined as EQD2, which results in a TCP value of 50% and \(\bf{γ}\) is a dimensionless parameter, defining the maximum normalized value of the dose-response gradient.
For an inhomogeneous dose distribution {D} within the tumour of volume V, the overall tumour control probability TCP is calculated according to:
\( TCP({D},V) = \prod_{i=1}^N[P(D_{i})]^{v_{i}/V} \)
Now, let’s plot the TCP for a homogeneous dose distribution with pyRadiobiology:
from pyradiobiology import *
import matplotlib.pyplot as plt
import numpy as np
doses = DoseBag(data=[*np.arange(start=0, stop=25, step=0.01)],
unit=DoseUnit.GY,
dose_type=DoseType.EQD2)
model = TcpEmpirical(d50=Dose.gy(10, DoseType.EQD2),
gamma=2.63)
tcp_voxels = model.voxel_response(doses)
plt.plot(doses.data, tcp_voxels, linewidth=4)
plt.xlabel("EQD2 (Gy)")
plt.ylabel("TCP")
plt.grid()
plt.show()The output:
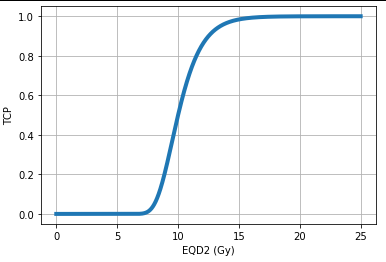
The TCP calculation for an inhomogeneous dose distribution can be performed as follows. Here, we have a tumor with two regions of 15 cc and 20 cc. The regions receive 70 Gy and 65 Gy, respectively. Further, assumptions are \( α/β = 3.0 Gy \) and the number of fractions, nfx = 40.
from pyradiobiology import *
tcpmodel = TcpEmpirical(
d50=Dose.gy(55, dose_type=DoseType.EQD2),
gamma=6.7)
dose_array = DoseBag.create(data=[70, 65],
unit=DoseUnit.GY,
dose_type=DoseType.PHYSICAL_DOSE)
volume_array_in_cc = [15, 20]
tcp = tcpmodel.response_from_pysical_dose(
dose_array_in_physical_dose=dose_array,
volume_array=volume_array_in_cc,
ab_ratio=Dose.gy(3.0),
nfx=40)
print(f"from physical dose, calculated TCP = {round(tcp, 4)}")
#self.assertEqual(0.9266, round(tcp, 4))So, in the above example you can also use the (dose, volume) tuples/pairs derived by a differential Dose-Volume-Histogram (DDVH).